We will determine the solution as follows:
*First: From the text, we have the following expressions:
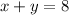
&
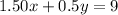
Here x represents apples and y represents bananas.
*Second: From the first expression, we solve for either x or y, that is [I will solve for ]:
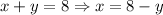
*Third: Now, using the value for x, we replace in the second expression and solve for y, that is:
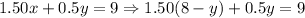
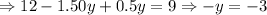
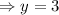
*Fourth: We replace the found value of y on the first expression and solve for x:
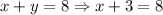
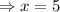
So, the number of apples was 5 and the number of bananas was 3.