Question

14#An ecologist randomly samples 12 plants of a specific species and measures their heights. He finds that this sample has a mean of 14 cm and a standard deviation of 4 cm. If we assume that the height measurements are normally distributed, find a 95% confidence interval for the mean height of all plants of this species. Give the lower limit and upper limit of the 95% confidence interval. Carry your intermediate computations to at least three decimal places. Round your answers to one decimal place. (If necessary, consult a list of formulas.)Lower limit:Upper limit:

Answer 1

Answer:

Lower limit: 11.7 cm

Upper limit: 16.263

Step-by-step explanation:

The formula to find the lower and upper limits of the confidence interval (given the data is normally distributed) is :

`CI=\mu\pm Z^*(\sigma)/(√(n))`

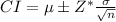
Where:

• μ = sample mean

,

• σ = sample standard deviation

,

• Z* = critical value of the z-distribution

,

• n = is the sample size

In this case:

• μ = 14cm

• σ = 4cm

,

• n = 12

The critical value of the z-distribution for a confidence interval of 95% is Z* = 1.96

Now, we can use the formula above to find the upper and lower limit:

`CI=14\pm1.96\cdot(4)/(√(12))=14\pm(98√(3))/(75)=(1050\pm98√(3))/(75)`

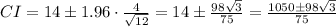
Thus:

`Lower\text{ }limit=(1050-98√(3))/(75)\approx11.736cm`
`Upper\text{ }limit=(1050-98√(3))/(75)\approx16.263cm`

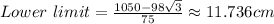
Rounded to one decimal:

Lower limit: 11.7cm

Upper limit: 16.3cm