ANSWER
Solution: b = 3
It is extraneous
Step-by-step explanation
We want to solve the equation given and to see if there are any extraneous solutions.
We have:

That is the solution to the equation.
To find if the solution is extraneous, we will insert the value of b = 3 into the original equation.
That is:
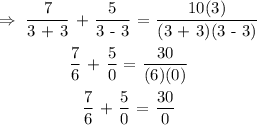
An extraneous solution is a solution that derives from solving a rational equation but does not exactly satisfy the original equation, that is, it is invalid for the equation.
By inserting b = 3 into the equation, we see that the equation is undefined.
Therefore, since b = 3 is a solution, but it does not satisfy the equation, it is an extraneous solution.