The midpoint for segment PQ can be calculated as:
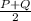
Then, the midpoint of PQ is:
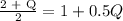
Additionally, PQ can be calculated as:

So:
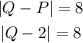
It means that:

Solving for Q, we get:
Q = 8 + 2 = 10 or Q = 2 - 8 = -6
Finally, replacing these values on the initial equation for the midpoint, we get:
If Q = 10, then:
midpoint = 1 + 0.5(10) = 1 + 5 = 6
If Q = -6, then:
midpoint = 1 + 0.5(-6) = 1 - 3 = -2
The possible midpoints for PQ are 6 and -2