The Solution To Question Number 10:
The question says what operations would the set of quadratics be closed under.
Let the sets of quadratics be
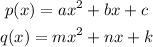
The set of two quadratics (polynomials) is closed under Addition.
Step-by-step explanation:
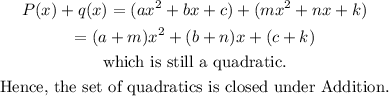
The set of two quadratics is closed under Subtraction.

The set of quadratics is not closed under Multiplication.
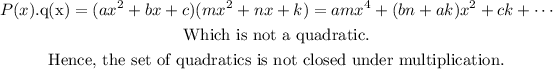
The set of quadratics is not closed under Division.
