The line given passes through two points. These are (-6,0) and (0,-8).
Remember that two lines are perpendicular if the product of their slopes is -1. So, the first thing we're going to do is to find the slope of the line given.
The slope between two points (x1,y1) and (x2,y2) can be found using the formula:

If we replace our values:
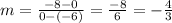
To find other perpendicular line to this one, we have to find a number which multiplication with -4/3 is -1.
This number is clearly 3/4. Because
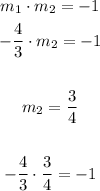
Therefore, the slope of the perpendicular line must be 3/4, and the original slope is -4/3.
If we graph this: