Question

given that the measure of arc AD=(17×+2), measure of arc AC=(7×-10),and measure of angle ABC=(4×+15) find the measure of angle ABC

Answer 1

In the given figure, angle ABC is formed by a tangent and a secant.

The angle formed by tangent and secant is given by

`m\angle ABC=(1)/(2)(m\bar{AD}-m\bar{AC})`

Where mAD and mAC are the intercepted arcs.

For the given case,

`\begin{gathered} m\angle ABC=(4x+15)\degree \\ m\bar{AD}=(17x+2)\degree \\ m\bar{AC}=(7x-10)\degree \end{gathered}`

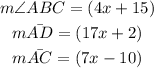
Let us substitute the given values into the above formula and solve for x

`\begin{gathered} m\angle ABC=(1)/(2)(m\bar{AD}-m\bar{AC}) \\ (4x+15)\degree=(1)/(2)\lbrack(17x+2)\degree-(7x-10)\degree\rbrack \\ 2\cdot(4x+15)\degree=(17x+2)\degree-(7x-10)\degree \\ 8x+30=17x+2-7x+10 \\ 8x-17x+7x=2+10-30 \\ -2x=-18 \\ x=(-18)/(-2) \\ x=9 \end{gathered}`

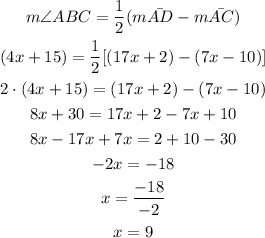
The value of x is 9

So, the measure of angle ABC is

`\begin{gathered} m\angle ABC=4x+15 \\ m\angle ABC=4(9)+15 \\ m\angle ABC=36+15 \\ m\angle ABC=51\degree \end{gathered}`

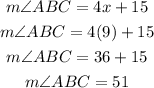
Therefore, the measure of angle ABC is 51°