The Law of Cosines
Let a,b, and c be the length of the sides of a given triangle, and x the included angle between sides a and b, then the following relation applies:
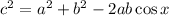
The triangle shown in the figure has two side lengths of a=4 and b=5. The included angle between them is x=100°. We can find the side length c by substituting the given values in the formula:
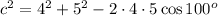
Calculating:
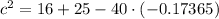
![\begin{gathered} c^2=47.946 \\ c=\sqrt[]{47.946}=6.92 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7s7vs45ull4945krf9rk1hyh1d1mxogcmx.png)
Now we can apply the law of the sines:
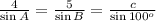
Combining the first and the last part of the expression above:
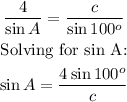
Substituting the known values:
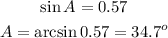
The last angle can be ob