Question

Solve the triangle for the missing sides and angles. Round all side lengths to the nearest hundredth. (Triangle not to scale.)

Answer 1

The Law of Cosines

Let a,b, and c be the length of the sides of a given triangle, and x the included angle between sides a and b, then the following relation applies:

`c^2=a^2+b^2-2ab\cos x`

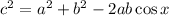
The triangle shown in the figure has two side lengths of a=4 and b=5. The included angle between them is x=100°. We can find the side length c by substituting the given values in the formula:

`c^2=4^2+5^2-2\cdot4\cdot5\cos 100^o`

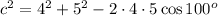
Calculating:

`c^2=16+25-40\cdot(-0.17365)`
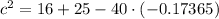
`\begin{gathered} c^2=47.946 \\ c=\sqrt[]{47.946}=6.92 \end{gathered}`

Now we can apply the law of the sines:

`(4)/(\sin A)=(5)/(\sin B)=(c)/(\sin 100^o)`

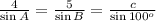
Combining the first and the last part of the expression above:

`\begin{gathered} (4)/(\sin A)=(c)/(\sin100^o) \\ \text{Solving for sin A:} \\ \sin A=(4\sin100^o)/(c) \end{gathered}`

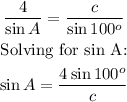
Substituting the known values:

`\begin{gathered} \sin A=0.57 \\ A=\arcsin 0.57=34.7^o \end{gathered}`

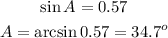
The last angle can be ob