Question

A horizontal rope is attached from a truck to a 1475-kg car. As the truck tows the car on a horizontal straight road, the rope will break if the tension is greater than 2551 N. Ignoring friction, what is the maximum possible acceleration of the truck if the rope does not break?

Answer 1

Given data

*The given mass of the car is m = 1475 kg

*The maximum tension is T = 2551 N

The formula for the maximum possible acceleration of the truck is given by Newton's second law as

`\begin{gathered} T=ma_(\max ) \\ a_(\max )=(T)/(m) \end{gathered}`

Substitute the known values in the above expression as

`\begin{gathered} a_(\max )=(2551)/(1475) \\ =1.72m/s^2 \end{gathered}`

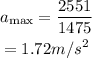
Hence, the maximum possible acceleration of the truck is a_max = 1.72 m/s^2