Question

What interest will be earned if $11,000.00 is invested for 3 years at 11% compounded semi-annual?You would earn $ in interest. (Round to 2 decimal places.)

Answer 1

$4,167.27

Explanation:

The amount, A(n) in an account for a Principal invested at compound interest is calculated using the formula:

`\begin{gathered} A(n)=P(1+(r)/(k))^(nk)\text{ }where=\begin{cases}P=Prin\text{cipal} \\ r=\text{Annual Interest Rate} \\ k=\text{Compounding Period}\end{cases} \\ n=nu\text{mber of years} \end{gathered}`

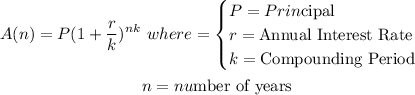
In the given problem:

• P = $11,000.00

,

• r=11% = 0.11

,

• n= 3 years

,

• k=2 (semi-annual)

Substitute these into the formula:

`\begin{gathered} A(n)=11,000(1+(0.11)/(2))^(2*3) \\ =11,000(1+0.055)^6 \\ =11,000(1.055)^6 \\ =\$15,167.27 \end{gathered}`

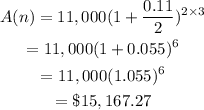
Next, we find the interest earned.

`\begin{gathered} \text{Interest}=\text{Amount}-\text{Prncipal} \\ =15167.27-11000 \\ =\$4,167.27 \end{gathered}`

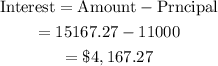
You would earn $4,167.27 in interest (rounded to 2 decimal places).