Question

The half-life of a radioactive isotope is the time it takes for quantity of the isotope to be reduced to half its initial mass. Starting with 175 grams of a radioactive isotope, how much will be left rafter 5 half-lives? Round your answer to the nearest gram

Answer 1

Exponential Decay

The model for the exponential decay of a quantity Mo is:

`M=M_o\cdot e^(-\lambda t)`

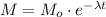
Where λ is a constant and t is the time.

The half-life of a radioactive isotope is the time it takes to halve its initial mass. It can be calculated by making M = Mo/2 and solving for t:

`\begin{gathered} (M_o)/(2)=M_o\cdot e^(-\lambda t) \\ \text{Simplifying:} \\ e^(-\lambda t)=(1)/(2) \\ \text{Taking natural log:} \\ -\lambda t=-\log 2 \\ t=(\log 2)/(\lambda) \end{gathered}`

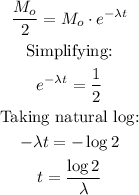
It's required to calculate the remaining mass of an isotope of Mo = 175 gr after 5 half-lives have passed, that is. we must calculate M when t is five times the value calculated above.

Substituting in the model:

`M=175gr\cdot e^{-\lambda\cdot(5\log 2)/(\lambda)}`

Simplifying (the value of λ cancels out):

`\begin{gathered} M=175gr\cdot e^(-5\log 2) \\ \text{Calculating:} \\ M=175gr\cdot0.03125 \\ M=5.46875gr \end{gathered}`

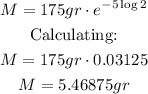
Rounding to the nearest gram, 5 grams of the radioactive isotope will be left after the required time.