Given the geometric progression below
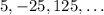
The nth term of a geometric progression is given below
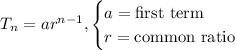
From the geometric progression, we can deduce the following
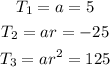
To find the value of r, we will take ratios of two consecutive terms
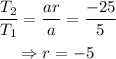
To find the 9th term of the geometric, we will have that;

Hence, the 9th term of the geometric progression is 1953125