Given the graph of a polynomial function:
We will find the following:
A. Find the zeros and state the multiplicity of each zero
The zeros of the function are the points of the intercept between the x-axis and the graph of the function
as shown, there are 3 points of intersection (3 zeros)
x = -1, multiplicity = 3
x = 1, multiplicity = 2
x = 2, multiplicity = 1
B. Write an equation expressed as the product of factors, of a polynomial function for the graph Using A leading coefficient of 1 or -1 and make the degree of F as small as possible.
Form A, the factors of the function will be:
(x+1), (x-1), and (x-2)
The equation of the function will be:
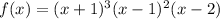
C. Use both the equation in part B and graph to find the Y-intercept
The y-intercept is the value of (y) when (x = 0)
So, substitute with x = 0
So,
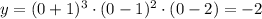
So, the answer will be: y-intercept = -2