To solve the exercise, you can use the formula of the binomial distribution:

So, in this case, we have:

Because "success" is that there are defective cameras, 6 defective cameras out of 10 in total.
For part A, we have:
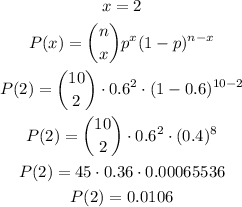
Therefore, the probability of getting 2 defective cameras is 0.0106.
For part B, we have:

Therefore, the probability of getting one defective camera is 0.0016.