Given the table showing the number of days since wound began to heal and area of wound in square millimeters
To determine the statement that are correct from the option provided
From the table shown it can be seen that as the day increases by 1, the area of wound in square millimeters decreases by a common ratio of
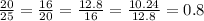
Suppose that an expression to represent the area of wound is
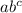
The modelled expression from the table is
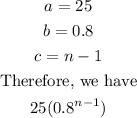
Let us use the modelled expression to verify each of the given conditions
The modelled expression can be simplified as shown below:

Then, we have the modelled expression becomes
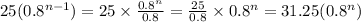
From the two modelled expression we can see that
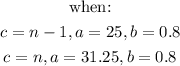
Then we can conclude that the two conditions that are true from the options are
If the value of c = n, the value of a is 31.25, and
If the value of c = n, the value of b is 0.8