Question

a company produces very unusual CD's for which the variable cost is 8$ per CD and the fixed costs are $30000. They will sell the CD's for $63 each. Let x be the number of CD's produced. Write the total cost C as a function of the number of CD's produced.C=$___Write the total revenue R as a function of the number of CD's produced R=$_______Write the total profit P as a function of the number of CD's producedP=$______Find the number of CD's which must be produced to break even.The number of CD's which must be produced to break even is_______

Answer 1

Remember that to model this kind of problems, we can use the equation of a straight line

`y=mx+b`

Where:

• b, are the fixed costs

,

• x ,represents what varies

,

• m, is the cost of what varies

1. Therefore, using the data provided, we can model the cost of production with a function where:

• x ,is the numbers of CD's produced

,

• C, is the cost of producing those CD's

`C=8x+30000`

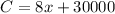
2. To model the revenue, we'll have to take into account that every CD sells at $68. Therefore, the money collected by selling the x CD's produced is:

`R=63x`

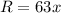
Where:

• x ,its the number of CD's produced and sold

,

• R, is the total revenue

3. To get the profit, we'll have to substract the production cost to the money collected by the sale. Remember we already have two expressions, in terms of x, that describe both situations. Therefore,

`\begin{gathered} P=R-C \\ \rightarrow P=63x-(8x+30000)\rightarrow P=63x-8x-30000 \\ \rightarrow P=55x-30000 \end{gathered}`

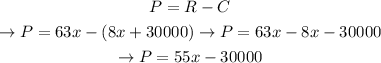
Where:

• x ,its the number of CD's produced and sold

,

• P, is the total revenue

4. In order to break even, the revenue (R) has to be equal to the cost of production (C), Thus,

`\begin{gathered} R=C\rightarrow63x=8x+30000 \\ \rightarrow63x-8x=30000 \\ \rightarrow55x=30000\rightarrow x=(30000)/(55) \\ x=545.5 \\ \text{Rounding to closest integer,} \\ x=546 \end{gathered}`

Therefore, 546 CD's would have to be produced to break even.