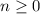From the recursive formula:
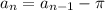
we notice that the common difference of the sequence is -pi. Now we know that the first term is 7, then the explicit formula is:
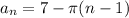
when
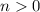
We can relabel this sequence if we assume we start at zero, in this case the sequence will be:
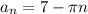
when: