Step-by-step explanation
To find the cutoff amount of annual speeding ticket revenue that separates the highest five percent of revenue-generating officers from the other ninety-five percent.
We will need to find
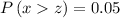
Therefore; using a z score calculator, this gives;
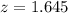
We can then find the cutoff amount z using the formula below;
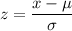
Since
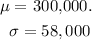
Therefore, we will have

Answer: 395410