The probability of a successful batting is 0.341; we need to find the probability of at least 1 hit within the first 5 at-bats; thus,
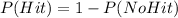
Therefore, we need to calculate the probability of not hitting the ball within the first 5 at-bats.
The binomial distribution states that

Thus, in our case,
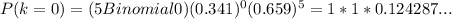
Then,
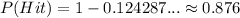
Therefore, the answer is 0.876