Question

Select the correct answer from each drop-down menu.Glven: W(-1, 1), X(3, 4), Y(6, 0), and Z(2, -3) are the vertices of quadrilateral WXYZ.Prove: WXYZis a square.

Answer 1

all four sides have a length of 5

Step-by-step explanation

The distance between two points (x₁, y₁) and (x₂, y₂) is,

`d=√((x_1-x_2)^2+(y_1-y_2)^2)`

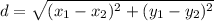
Let's find the distance between each pair of points, WX, XY, YX, and WZ,

`WX=√((3-(-1))^2+(4-1)^2)=√((3+1)^2+(4-1)^2)=√(4^2+3^2)=√(16+9)=√(25)=5`
`XY=√((6-3)^2+(0-4)^2)=√((3)^2+(-4)^2)=√(3^2+4^2)=√(9+16)=√(25)=5`
`YZ=√((2-6)^2+(-3-0)^2)=√((-4)^2+(-3)^2)=√(4^2+3^2)=√(16+9)=√(25)=5`
`WZ=√((2-(-1))^2+(-3-1)^2)=√((2+1)^2+(-4)^2)=√(3^2+4^2)=√(9+16)=√(25)=5`

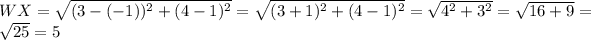
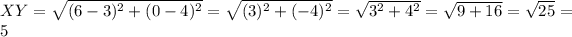
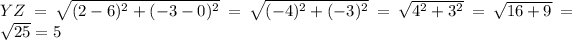
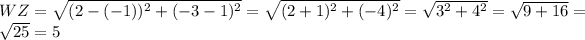
Hence, using the distance formula we found that all four sides have a length of 5.