Question

What is the 100th term of the arithmetic sequence below? 2x, 3x + 4, 13x - 1

Answer 1

We are given an arithmetic progression and are requested to find the 100th term of the progression. We need to find the value of x from the question by equating differences.

`\begin{gathered} T_2-T_1=T_3-T_2 \\ 3x+4-2x=13x-1-(3x+4)=13x-1-3x-4 \\ x+4=10x-5 \\ \text{Collecting like terms gives us:} \\ 10x-x=4+5 \\ 9x=9 \\ x=1 \end{gathered}`

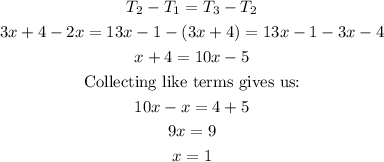
Now we will find the actual value of our terms.

`\begin{gathered} T_1=a=2(1)=2 \\ T_2=3(1)+4=7 \\ T_3=13(1)-1=12 \\ \text{Therefore,} \\ \text{ d = }T_2-T_1=T_3-T_2 \\ d=7-2=12-7=5 \end{gathered}`

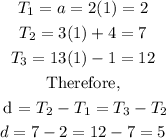
Common difference, d = 5

Lastly, we employ our AP formula to find the 100th term.

`\begin{gathered} Tn=a+(n-1)d \\ T_(100)=2+(100-1)5 \\ T_(100)=2+(99)5=497 \end{gathered}`

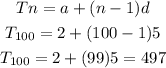
The 100th term is 497