Question

(c) Given that q= 8d^2, find the other two real roots.

Answer 1

Polynomials

Given the equation:

`x^5-3x^4+mx^3+nx^2+px+q=0`

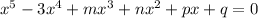
Where all the coefficients are real numbers, and it has 3 real roots of the form:

`x_1=\log _2a,x_2=\log _2b,x_3=\log _2c`

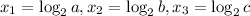
It has two imaginary roots of the form: di and -di. Recall both roots must be conjugated.

a) Knowing the sum of the roots must be equal to the inverse negative of the coefficient of the fourth-degree term:

`\begin{gathered} \log _2a+\log _2b+\log _2c+di-di=3 \\ \text{Simplifying:} \\ \log _2a+\log _2b+\log _2c=3 \\ \text{Apply log property:} \\ \log _2(abc)=3 \\ abc=2^3 \\ abc=8 \end{gathered}`

b) It's additionally given the values of a, b, and c are consecutive terms of a geometric sequence. Assume that sequence has first term a1 and common ratio r, thus:

`a=a_1,b=a_1\cdot r,c=a_1\cdot r^2`

Using the relationship found in a):

`\begin{gathered} a_1\cdot a_1\cdot r\cdot a_1\cdot r^2=8 \\ \text{Simplifying:} \\ (a_1\cdot r)^3=8 \\ a_1\cdot r=2 \end{gathered}`

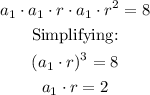
As said above, the real roots are:

`x_1=\log _2a,x_2=\log _2b,x_3=\log _2c`

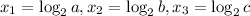
Since b = a1*r, then b = 2, thus:

`x_2=\log _22=1`

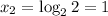
One of the real roots has been found to be 1. We still don't know the others.

c) We know the product of the roots of a polynomial equals the inverse negative of the independent term, thus:

`\log _2a_1\cdot2\cdot\log _2(a_1\cdot r^2)\cdot(di)\cdot(-di)=-q`

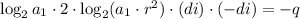
Since q = 8 d^2:

`\begin{gathered} \log _2a_1\cdot2\cdot\log _2(a_1\cdot r^2)\cdot(di)\cdot(-di)=-8d^2 \\ \text{Operate:} \\ 2\log _2a_1\cdot\log _2(a_1\cdot r^2)\cdot(-d^2i^2)=-8d^2 \\ \log _2a_1\cdot\log _2(a_1\cdot r^2)=-8 \end{gathered}`

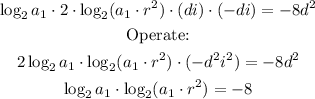
From the relationships obtained in a) and b):

`a_1=(2)/(r)`

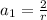
Substituting:

`\begin{gathered} \log _2((2)/(r))\cdot\log _2(2r)=-8 \\ By\text{ property of logs:} \\ (\log _22-\log _2r)\cdot(\log _22+\log _2r)=-8 \end{gathered}`

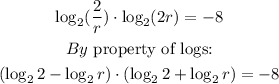
Simplifying:

`\begin{gathered} (1-\log _2r)\cdot(1+\log _2r)=-8 \\ (1-\log ^2_2r)=-8 \\ \text{Solving:} \\ \log ^2_2r=9 \end{gathered}`

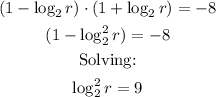
We'll take the positive root only:

`\begin{gathered} \log _2r=3 \\ r=8 \end{gathered}`

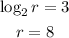
Thus:

`a_1=(2)/(8)=(1)/(4)`

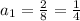
The other roots are:

`\begin{gathered} x_1=\log _2(1)/(4)=-2 \\ x_3=\log _216=4 \end{gathered}`

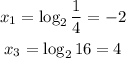
Real roots: -2, 1, 4