A quadratic function describes the relationship between the number of products x and the overall profits for a company.
The roots of the quadratic function are given as x = 0 and x = 28. We also know the graph's vertex is located at (14, -40).
The quadratic equation can be written in terms of its roots x1 and x2 as:
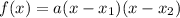
Substituting the given values:
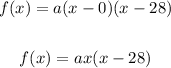
We can find the value of a by plugging in the coordinates of the vertex:
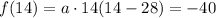
Solving for a:

Substituting into the equation:
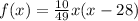
The graph of the function is given below:
The company actually loses money on their first few products, but once they hit 28 items, they break even again.
The worst-case scenario is that they produce 14 items, as they will have a profit of -40 dollars. The first root tells us the profit will be 0 when 0 products are sold.