Answer:
Plane: 165 miles per hour
Wind: 15 miles per hour
Step-by-step explanation:
Let's call x the speed of the plane in still air and y the speed of the wind.
Additionally, the velocity is equal to distances over time. So, when the plane is flying against the wind, we can write the following equation:
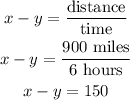
Because x - y is the total velocity of the plane when it is flying against the wind.
On the other hand, when the plane flies with the wind, we get:
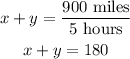
So, we have the following system of equations:
x - y = 150
x + y = 180
Adding both equations, we get:
x - y = 150
x + y = 180
2x + 0 = 330
Solving for x:
2x = 330
2x/2 = 330/2
x = 165
Finally, Replace x by 165 on the second equation and solve for y as:
x + y = 180
165 + y = 180
165 + y - 165 = 180 - 165
y = 15
Therefore, the speed of the plane in still air is 165 miles per hour and the speed of the air is 15 miles per hour.