We have to write as inequality the following
"All real numbers more than 4 units away from x"
"4 units away from x" means four units plus x. So, the expression would be
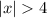
Where x represents real numbers.
This expression is referring to all real numbers more than 4 units and less than -4 units because according to the property of absolute values for inequalities, we have
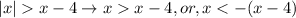
This is represented in the following graph to see it better
For x=1
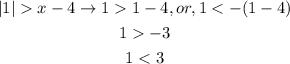
Both results are true.
To find this absolute value inequality we used the following property
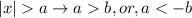
Where the absolute value inequality has "more than" we rewrite the expression in two inequalities.