Step-by-step explanation
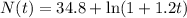
we have a function where the number of microbes ( N) depends on the time(t)
hence
Step 1
a.) How many microbes are present initially?
to know this, we need replace time I= t = zero, because it was "initially"
so
when t=0
replace.
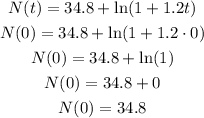
so, initially there were 34.8 microbes
Step 2
b)How fast are the microbes increasing after 10 hours?
to know this, let t=10
so

therefore , after 10 hours the number of microbes is 37.36
I hope this helps you