Question

A train car with a mass of 10kg and speed of 10 m/s is traveling to the right. Another train car with a mass of 20kg is moving to the left at -40 m/s. After the collision, the 10 kg train car is now moving at -20 m/s and we need to find the Velocity of the 20 kg train car.

Answer 1

When two particles collide and the masses of the particles are given, as well as the initial and final velocity of one particle and one of the velocities of the second particle, then the remaining velocity of the second particle is given by the expression:

`v_2^(\prime)=(m_1v_1+m_2v_2-m_1v_1)/(m_2)`

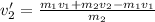
Which can be deduced from the Law of Conservation of Linear Momentum.

In the given problem, the initial and final velocities of the train car with mass 10kg are given, as well as the initial velocity of the 20kg car:

`\begin{gathered} m_1=10kg \\ v_1=10(m)/(s) \\ v_1^(\prime)=-20(m)/(s) \\ \\ m_2=20kg \\ v_2=-40(m)/(s) \\ v_2^(\prime)=\text{ unknown} \end{gathered}`

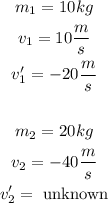
Replace those values into the given equation to find v₂':

`\begin{gathered} v_2^(\prime)=((10kg)(10(m)/(s))+(20kg)(-40(m)/(s))-(10kg)(-20(m)/(s)))/(20kg) \\ \\ \Rightarrow v_2^(\prime)=-25(m)/(s) \end{gathered}`

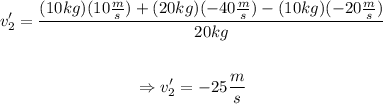
Therefore, the velocity of the 20kg train car after the collision, is: -25 m/s.