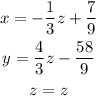Question

3. Solve the system using elimination (not substitution or matrices). negative 2 x plus y minus 2 z equals negative 8A N D7 x plus y plus z equals negative 1A N D5 x plus 2 y minus z equals negative 91. If the system has a single solution, write the solution as an ordered triple, (x, y, z).2. If the system has infinite solutions, write the solutions IN TERMS OF z.The solution should look something like left parenthesis 3 minus 3 z comma space minus 1 plus 7 z comma space z right parenthesis but not like left parenthesis negative 6 plus 3 y comma space y comma space 2 minus 5 y right parenthesis or not like left parenthesis x comma space 3 plus 5 x comma space minus 1 plus 4 x right parenthesis. None of these are the solution, they are just examples of what the answer could look like and not look like.3. Be sure to show all appropriate work. Extraneous work may be counted against you. Your handwritten work should include the steps used to find the solution. You should label your steps with how you combined your equations, like 2E1+E3. Solutions with no work will receive no credit.

Answer 1

Given the system of equation

`\begin{gathered} -2x+y-2z=-8\ldots\ldots\ldots\text{.}(1) \\ 7x+y+z=-1\ldots\ldots\ldots\text{..}(2) \\ 5x+2y-z=-9\ldots\ldots\ldots\text{.}(3) \end{gathered}`

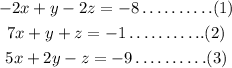
step 1: Make z the subject of the formula in equations (2)

`z=-1-7x-y\ldots\ldots\ldots(2)`

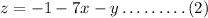
step 2: Substitute the value of z obtained into equation (1)

10

step 3: Substitute the value of z obtained in step 1 into equation (3)

`\begin{gathered} 5x+2y-(-1-7x-y)=-9 \\ 5x+2y+1+7x+y=-9 \\ 12x+3y=-10\ldots\ldots\ldots\text{.}(5) \end{gathered}`

step 4: Solve equations (4) and (5) simultaneously,

`\begin{gathered} 12x+3y=-10\ldots\ldots\ldots\text{.}(4) \\ 12x+3y=-10\ldots\ldots\ldots\text{.}(5) \\ \text{subtract equation (5) from (4)} \\ (12x-12x)+(3y-3y)=-10-(-8) \\ 0\text{ + 0 = }-10+10 \\ 0=0 \end{gathered}`

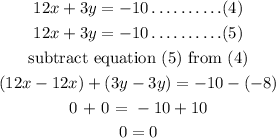
Therefore, the system has infinite solutions

The solution in terms of z is

`\begin{gathered} x=-(1)/(3)z+(7)/(9) \\ y=(4)/(3)z-(58)/(9) \\ z=z \end{gathered}`