Question

Find the rule for the following sequence. Then find the 45th term.

Answer 1

`a_(45)=221`

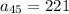
Explanation:

Arithmetic sequences are represented by the following equation;

`\begin{gathered} a_n=a_1+(n-1)d \\ where, \\ a_1=\text{ first term} \\ d=\text{ common difference} \\ n=\text{ nth term} \end{gathered}`

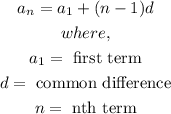
The common difference is the difference between the consecutive terms:

`\begin{gathered} d=6-1=5 \\ d=11-6=5 \\ d=16-11=5 \end{gathered}`

Therefore, the equation that represents this sequence:

`a_n=1+5(n-1)`

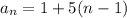
Now, if we want to find the 45th term, substitute n=45:

`\begin{gathered} a_(45)=1+5(45-1) \\ a_(45)=1+5*(44) \\ a_(45)=1+220 \\ a_(45)=221 \end{gathered}`