Question

Given points C(-3,-8) and D(-6.5,-4.5), find the coordinate of the point that is 2/3 of the way from C to D.

Answer 1

(-16/3,-17/3)

Step-by-step explanation:

Let the point which is 2/3 of the way from C to D = X

It means that point X divides the line segment CD internally in the ratio 2:1.

To determine the coordinate of point X, we use the section formula for internal division of a line segment:

`(x,y)=\left\{ (mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right\}`
`\begin{gathered} (x_(1,)y_1)=(-3,-8) \\ (x_2,y_2)=(-6.5,-4.5) \\ m\colon n=2\colon1 \end{gathered}`

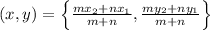
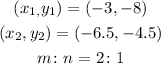
Substituting these values into the formula above, we have:

`X(x,y)=\left\{ (2(-6.5)+1(-3))/(2+1),(2(-4.5)+1(-8))/(2+1)\right\}`

We then simplify:

`\begin{gathered} X(x,y)=\left\{ (-13-3)/(3),(-9-8)/(3)\right\} \\ =\left\{ (-16)/(3),(-17)/(3)\right\} \end{gathered}`

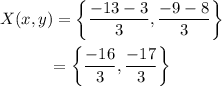
Therefore, the exact coordinate of the point that is 2/3 of the way from C to D is (-16/3,-17/3).