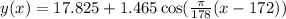Question

The graph below and to the left shows the time of sunsets occurring every other day during September in a certain town. The graph at the lower right shows the time of sunsets on either the 21st or 22nd day of each month for an entire year in the same town. The vertical axis is scaled to reflect hours after midnight. Round to 4 decimal places. a) Find a linear model for the data in the graph at the left. Include units to your variables. b) Find a cosine model for the data in the graph to the right. Include units to your variables,

Answer 1

A) Given the points (1,18.35) and (29,17.5), we can find the linear model with the following formulas:

`\begin{gathered} \text{slope:} \\ m=(y_2-y_1)/(x_2-x_1)=(71.5-18.35)/(29-1)=(-0.85)/(28)=-0.03 \\ \text{equation of the line:} \\ y-y_1=m(x-x_1) \\ \Rightarrow y-18.35=-0.03(x-1)=-0.03x+0.03 \\ \Rightarrow y=-0.03x+0.03+18.35=-0.03x+18.38 \\ y=-0.03x+18.38 \end{gathered}`

therefore, the linear model is y = -0.03x+18.38

B)We have the general cosine model:

`y(t)=A+B\cos (\omega(t-\phi))`

Where A is the vertical shift, B is the amplitude, w is the frequency and phi is the phase shift.

First, we can find the vertical shift with the following formula:

`A=(y_(\max )+y_(\min ))/(2)`

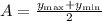
in this case, we have that the maximum value for y is 19.47 and the minimum value for y is16.18, then:

`A=(19.47+16.18)/(2)=17.825`

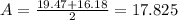
next, we can find the amplitud with the following formula:

`B=y_(\max )-A`

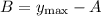
We have then:

`B=19.47-17.825=1.645`

Now, notice that the graph will repeat every 356 values for t, then, for the frequency we have the following expression:

`\omega=(2\pi)/(356)=(\pi)/(178)`

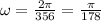
To find the phase shift, notice that for the point (172,19.47), we have the following:

`\begin{gathered} y(172)=19.47 \\ \Rightarrow17.825+1.645\cos ((\pi)/(178)(172-\phi))=19.47 \\ \Rightarrow1.645\cos ((\pi)/(178)(172-\phi))=1.645 \\ \Rightarrow\cos ((\pi)/(178)(172-\phi))=1 \end{gathered}`

notice that if the cosine equals 1, then its argument must equal to 0, then, we have:

`\begin{gathered} (\pi)/(178)(172-\phi)=0 \\ \Rightarrow172-\phi=0 \\ \Rightarrow\phi=172 \end{gathered}`

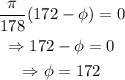
we have that the phase shift is phi = 172, then, the final cosine model is:

`y(x)=17.825+1.465\cos ((\pi)/(178)(x-172))`