Given that the pair of triangles are similar, then their corresponding sides are in proportion, this means that:
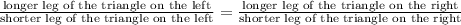
Substituting with the information of the diagram:
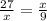
Cross multiplying:
![\begin{gathered} 27\cdot9=x\cdot x \\ 243=x^2 \\ \sqrt[]{243}=x \\ 15.58\approx x \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4i94kfiv3gd6120cpsyenhai0jbddmz5vr.png)
Considering the triangle on the left, and applying the Pythagorean theorem with c = y (the hypotenuse), a = 27, and b = x (the legs), we get:
![\begin{gathered} c^2=a^2+b^2 \\ y^2=27^2+x^2 \\ y^2=729+243 \\ y^2=972 \\ y=\sqrt[]{972} \\ y\approx31.18 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/d6kazjlpf5n9jv587kd2l3unowdo8kunm6.png)