For an investment compounded weekly at:
(A) 7.8%, it will take approximately 8.89 years to double.
(B) 13%, it will take approximately 5.36 years to double.
To find the time it takes for money to double when invested at a certain interest rate compounded periodically, you can use the formula for compound interest:
![\[ A = P * \left(1 + (r)/(n)\right)^(nt) \]](https://img.qammunity.org/2023/formulas/mathematics/college/tta1ll896pmjbyhzmtttdbgzm96c4lun3x.png)
Where:
- A is the amount after time t.
- P is the principal amount (initial investment).
- r is the annual interest rate (in decimal).
- n is the number of times the interest is compounded per year.
- t is the time the money is invested for (in years).
We want to solve for t when the initial amount doubles, so A = 2P.
Let's solve for t using the formula and the provided interest rates:
For (A) 7.8%$ compounded weekly:
- r = 0.078 (as a decimal)
- n = 52 (weeks in a year)
Using the formula
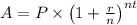 and substituting A = 2P to find t:
and substituting A = 2P to find t:
![\[ 2P = P * \left(1 + (0.078)/(52)\right)^(52t) \]](https://img.qammunity.org/2023/formulas/mathematics/college/olm55fg2ihzco0ca6dtz59b8k5zwdptxe8.png)
Simplify:
![\[ 2 = \left(1 + (0.078)/(52)\right)^(52t) \]](https://img.qammunity.org/2023/formulas/mathematics/college/pggualehm5n8vrsgrxs1xdtr2nicwpbv7w.png)
![\[ \left(1 + (0.078)/(52)\right)^(52t) = 2 \]](https://img.qammunity.org/2023/formulas/mathematics/college/g3260bd6ypaqk6e78s6eqibszku8quo17w.png)
Now solve for t:
![\[ 52t * \log\left(1 + (0.078)/(52)\right) = \log 2 \]](https://img.qammunity.org/2023/formulas/mathematics/college/1dr7g0elbxeuacux2gchn3vjten96z2qkc.png)
![\[ t = (\log 2)/(52 * \log\left(1 + (0.078)/(52)\right)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/tiomtv71xu5rqbj5x3gf0ig6xzkq3hsmm7.png)
![\[ t \approx 8.89 \]](https://img.qammunity.org/2023/formulas/mathematics/college/kgzjdkm7pfcghg3zq10tqb5u3xuon0mb90.png)
So, at an interest rate of 7.8 % compounded weekly, it will take approximately 8.89 years for the money to double.
For (B) 13% compounded weekly, you can apply the same formula with the new interest rate r = 0.13 and n = 52:
![\[ t = (\log 2)/(52 * \log\left(1 + (0.13)/(52)\right)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/spu7ou15sfkxmc97wt2nldzwdg6piees5l.png)
![\[ t \approx 5.36 \]](https://img.qammunity.org/2023/formulas/mathematics/college/xc4j60lughoi0fe26ye1pn9h3vc9jwtgel.png)
Therefore, at an interest rate of 13% compounded weekly, it will take approximately 5.36 years for the money to double.