Question

A right triangle has a hypotenuse of length 3.80 m, and one of its angles is 31.0°. What are the lengths of the following sides?

Answer 1

• (a)The length of the side opposite 31.0° is 1.96 meters.

,

• (b)The length of the side adjacent 31.0° is 3.26 meters.

Explanation:

In the right triangle:

• The length of the hypotenuse = 3.80 m

,

• Let the side ,opposite ,angle 31.0° = x

• Let the side ,adjacent ,angle 31.0° = y

(a)

From trigonometric ratios:

`\begin{gathered} \sin\theta=(Opposite)/(Hypotenuse) \\ \implies\sin31.0\degree=(x)/(3.80) \end{gathered}`

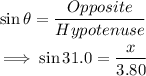
Cross multiply:

`\begin{gathered} x=3.80*\sin31.0\degree \\ x=1.9571 \\ x\approx1.96\;m \end{gathered}`

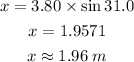
The length of the side opposite 31.0° is 1.96 meters.

(b)From trigonometric ratios:

`\begin{gathered} \cos\theta=(Adjacent)/(Hypotenuse) \\ \implies\cos31.0\degree=(y)/(3.80) \end{gathered}`

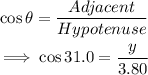
Cross multiply:

`\begin{gathered} y=3.80*\cos31.0\degree \\ y=3.2572 \\ y\approx3.26\;m \end{gathered}`

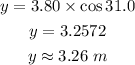
The length of the side adjacent 31.0° is 3.26 meters.