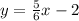First we can find the slope. The standard form of the equation of a line is:
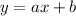
Where a is the slope and b is the intercept.
When 2 lines are perpendicular, the slopes are reciprocal and opposite to each other. If we write the given equation of the perpendicular line in the standard form we have:
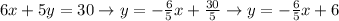
So you got the slope right, it's 5/6.
Now, with the given point we find the intercept. The point is x = -6 and y = -7, so we replace these values into the expression we have until now:
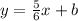
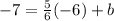
And solve for b
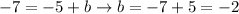
So the equation of the line is: