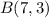By definition, the formula to find a Midpoint is:
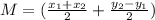
Where the coordinates of the first point are:
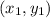
And the coordinates of the second point is:
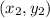
Let be the coordinates of the Midpoint:
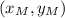
In this case, knowing coordinates of the point A and the Midpoint, you can set up the following equations:
- Equation 1:
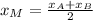
- Equation 2:
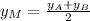
Choose the Equation 1, substiutute values and solve for x-coordinate of the endpoint B:
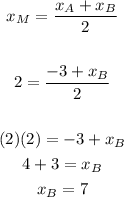
Now choose the Equation 2 and solve for the y-coordinate of the point B:
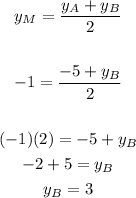
Therefore, the coordinates of P are: