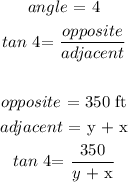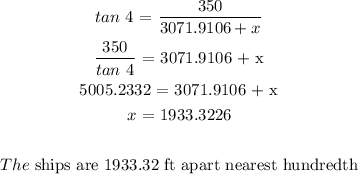Question

An observer in a lighthouse 350 ft above sea level observes two ships directly offshore. The angles of depression to the shops are 4 degree and 6.5 degree. How far apart are the ships?

Answer 1

Answer:

The two ships are 1933.32 ft apart

Step-by-step explanation:

Given:

The height of the lighthouse = 350 ft

The angles of depression to the ships are 4 degree and 6.5 degree

To find:

the distance between the two ships

To determine the distance, we will use an illustration of the situation

First we will find the value of y as we need to know this value to get x

To get y, we will apply tan ratio (TOA)

`\begin{gathered} tan\text{ 6.5\degree = }(opposite)/(adjacent) \\ opp\text{ = 350 ft} \\ adj\text{ = y} \\ tan\text{ 6.5\degree = }(350)/(y) \\ y(tan\text{ 6.5\degree\rparen= 350} \\ y\text{ = }\frac{350}{tan\text{ 6.5}} \\ y\text{ = 3071.9106 ft} \end{gathered}`

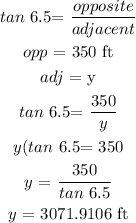
Next is to find x using tan ratio (TOA):

`\begin{gathered} angle\text{ = 4\degree} \\ tan\text{ 4\degree= }(opposite)/(adjacent) \\ \\ opposite\text{ = 350 ft} \\ adjacent\text{ = y + x} \\ tan\text{ 4\degree= }\frac{350}{y\text{ + x}} \end{gathered}`
`\begin{gathered} tan\text{ 4 = }(350)/(3071.9106+x) \\ \frac{350}{tan\text{ 4}}\text{ = 3071.9106 + x} \\ 5005.2332\text{ = 3071.9106 + x} \\ x\text{ = 1933.3226} \\ \\ The\text{ ships are 1933.32 ft apart \lparen nearest hundredth\rparen} \end{gathered}`