Step-by-step explanation:
We have the expression:
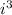
where i represents the complex number i defined as follows:
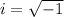
To find if i^3 is real or complex, we represent it as follows:
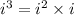
And we find the value of i^2 using the definition of i:
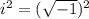
Since the square root and the power of 2 cancel each other

And therefore, using this value for i^2, we can now write i^3 as follows:
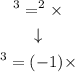
This simplifies to -i

Because -i is still a complex number, that means that i^3 is a complex number.
Answer: Complex