SOLUTION
Given the question in the question tab, the following are the solution steps to answer the question.
STEP 1: Define the variation that occurs in the Question.
Inverse Variation: Inverse variation is the relationship between two variables, such that if the value of one variable increases then the value of the other variable decreases.
STEP 2: Interpret the statements in the question tab
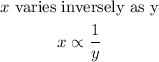
STEP 3: Get the constant of variation

STEP 4: Use the given values to get the equation relating x and y
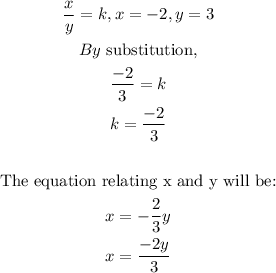
Hence, the equation relating x and y is:
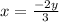
STEP 5: Find y when x=-1
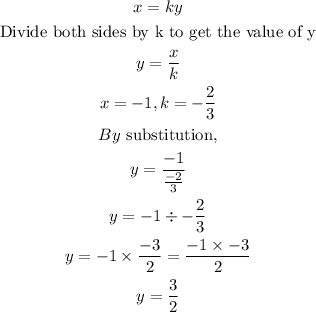
Hence, the value of y when x=-1 is 3/2