Question

A population of 2000 is decreasing by 4% each year. In how many years the population will be reduced in half?

Answer 1

the initial amount is 2000

the rate of change is 4%

t=time in years

Therefore we have the next exponential decay function

`\begin{gathered} y=2000(1-0.04)^t \\ y=2000(0.96)t \end{gathered}`

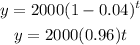
Half of the population is y=1000 so we need to find find the value of t

`1000=2000(0.96)^t`

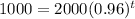
we need to isolate the t

`(1000)/(2000)=0.96^t`

`(1)/(2)=0.96^t`

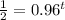
Using logarithms

`\begin{gathered} \ln ((1)/(2))=\ln (0.96^t) \\ \ln ((1)/(2))=t\ln (0.96^t) \end{gathered}`
`t=\frac{\ln ((1)/(2))}{\ln (0.96^{})}=16.98\approx17`

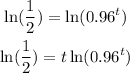
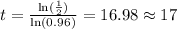
ANSWER

in 17 years the population will be reduced in half