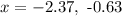Question

2x^2 +6x=-3 can you compute this?

Answer 1

The general formula for a quadratic equation is ax² + bx + c = 0.

To solve

`2x^2+6x=-3`

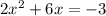
You can follow the steps.

Step 01: Write the equation in the general formula.

To do it, add 3 to each side of the equation.

`\begin{gathered} 2x^2+6x+3=-3+3 \\ 2x^2+6x+3=0 \end{gathered}`

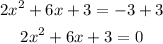
Step 02: Use the Bhaskara formula to find the roots.

The Bhaskara formula is:

`x=\frac{-b\pm\sqrt[]{\Delta}}{2\cdot a},\Delta=b^2-4\cdot a\cdot c`

In this question,

a = 2

b = 6

c = 2

So, substituting the values:

`\begin{gathered} \Delta=b^2-4\cdot a\cdot c \\ \Delta=6^2-4\cdot2\cdot3 \\ \Delta=36-24 \\ \Delta=12 \\ \\ x=\frac{-6\pm\sqrt[]{12}}{2\cdot2} \\ x=\frac{-6\pm\sqrt[]{2\cdot2\cdot3}}{4} \\ x=\frac{-6\pm2\cdot\sqrt[]{3}}{4} \\ x_1=\frac{-6+2\sqrt[]{3}}{4}=\frac{-3+\sqrt[]{3}}{2} \\ x_2=\frac{-6-2\sqrt[]{3}}{4}=\frac{-3-\sqrt[]{3}}{2} \end{gathered}`

Answer:

Exact form:

`x=\frac{-3-\sqrt[]{3}}{2},\frac{-3+\sqrt[]{3}}{2}`

Decimal form:

`x=-2.37,\text{ -0.63}`