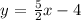Question

Which equation represents a line having a slope of 5/2 and a y intercept of (0,-4)

Answer 1

First you must know the standard equation of a line and this is expressed as:

`y\text{ = mx+c}`

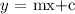
where:

m is the slope of the line

c is the intercept

Given

Slope m = 5/2

Next is to get the intercept c:

To do that, you will substitute m = 5/2 and the coordinate (0, -4) into the equation above as shown:

`\begin{gathered} -4\text{ = 5/2(0)+c} \\ -4\text{ = 0+c} \\ c\text{ = -4} \end{gathered}`

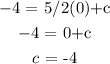
Next is to get the required equation by substituting m = 5/2 and c = -4 into the equation above as shown:

`\begin{gathered} y\text{ = mx + c} \\ y\text{ = }(5)/(2)x\text{ +(-4)} \\ y\text{ = }(5)/(2)x\text{ - 4} \end{gathered}`

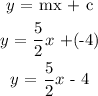
Hence the required equation is espressed as:

`y\text{ = }(5)/(2)x-4`