Question

A population forms a normal distribution with a meanof μ = 85 and a standard deviation of o = 24. Foreach of the following samples, compute the z-score forthe sample mean.a. M=91 for n = 4 scoresb. M=91 for n = 9 scoresc. M=91 for n = 16 scoresd. M-91 for n = 36 scores

Answer 1

Step-by-step explanation

In this problem, we have a population with a normal distribution with:

• mean μ = 85,

,

• standard deviation σ = 24.

We must compute the z-score for different samples.

The standard deviation of a sample with mean M and size n is:

`σ_M=(σ)/(√(n)).`

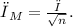
The z-score of the sample is given by:

`z(M,n)=(M-\mu)/(\sigma_M)=√(n)\cdot((M-\mu)/(\sigma))`

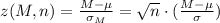
Using these formulas, we compute the z-score of each sample:

(a) M = 91, n = 4

`z(91,4)=√(4)\cdot((91-85)/(24))=0.5.`

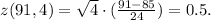
(b) M = 91, n = 9

`z(91,9)=√(9)\cdot((91-85)/(24))=0.75.`

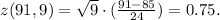
(c) M = 91, n = 16

`z(91,16)=√(16)\cdot((91-85)/(24))=1.`

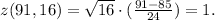
(d) M = 91, n = 36

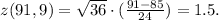
`z(91,9)=√(36)\cdot((91-85)/(24))=1.5.`Answer

a. z = 0.5

b. z = 0.75

c. z = 1

d. z = 1.5