Question

The instructions are: Write,evaluate,graph on a Number Line the following inequalities:Six increased by twice a number is no more than 20.

Answer 1

• Given the description "Six increased by twice a number is no more than 20", you need to know the following:

- In this case, the word "increased" indicates an Addition.

- The word "twice" indicates a Multiplication by 2.

- "No more than" indicates that six increased by twice a number must be less than or equal to 20.

- The inequality symbol whose meaning is "Less than or equal to" is:

`\leq`

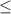
Knowing the information shown before, you can write the following expression to represent "Six increased by twice a number" (Let be "x" the unknown number):

`6+2x`

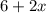
Therefore, you can write the following inequality that models the description given in the exercise:

`6+2x\leq20`

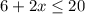
• Now you need to solve it:

1. Apply the Subtraction Property of Inequality by subtracting 6 from both sides of the inequality:

`\begin{gathered} 6+2x-(6)\leq20-(6) \\ \\ 2x\leq14 \end{gathered}`

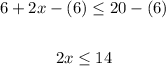
2. Apply the Division Property of Inequality by dividing both sides of the inequality by 2:

`\begin{gathered} (2x)/(2)\leq(14)/(2) \\ \\ x\leq7 \end{gathered}`

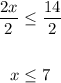
• In order to graph the solution on a Number Line, you can follow these steps:

- Since the inequality symbol indicates that "x" is less than 7, it indicates that 7 is included in the solution. Therefore, you must draw a closed circle over that value.

- Draw a line from the circle to the left.

Then, you get:

Hence, the answer is:

- Inequality:

`6+2x\leq20`

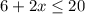
- Solution:

`x\leq7`

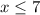
- Number Line: