Question

What is the measure of the angle at the bottom of home plate?

Answer 1

We will ave the following:

*First: We will determine the sum of all internal angles of the polygon:

`(n-2)\cdot180\Rightarrow(5-2)\cdot180=3\cdot180`
`=540`

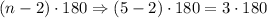
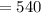
*Second: Now, that we know that the sum of all internal angles will be 540°, the following is true:

`90+90+135+135+\alpha=540`

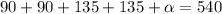
Now, we solve for alpha [The angle]:

`\Rightarrow\alpha=540-135-135-90-90\Rightarrow\alpha=90`

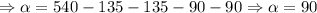
So, the measure of the angle at the bottom is 90°.