We are given two equations, one of which has an isolated variable
 .
.
That screams to me that substitution would be a prefered strategy here, compared to elimination, although both work.
That means we'll be substituting our value of
 , which is given as
, which is given as
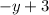 , into the first equation,
, into the first equation,
 .
.

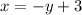

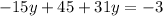
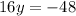
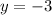
With this value, we can plug it back into either of the two equations to solve for
 , I'll be substituting it back into the second equation, since it's easier.
, I'll be substituting it back into the second equation, since it's easier.
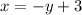
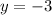
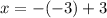
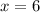
So our solution is
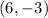 , and to check we can plug it back into the first equation.
, and to check we can plug it back into the first equation.


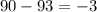
Which is true, so our solution is correct.
Hope this helps!