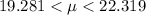Solution:
The confidence interval is expressed as
where

Given a 99% confidence interval for a sample size of 891 with a mean of 20.8 and a standard deviation of 17.6, this implies that
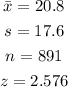
By substituting these values into the above equation, we have

Hence, we have