Question

Part AType an equation to represent the cost of the topsoil.Part BHow does the cost of the topsoil compare to the cost of the mulch?

Answer 1

Step 1

Write the equation of a line in slope point form

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

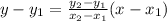
Where;

`\begin{gathered} y_2=\text{ 60} \\ x_2=2 \\ y_1=\text{ 30} \\ x_1=\text{ 1} \end{gathered}`

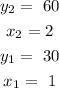
Step 2

Find the equation to represent the cost of the topsoil.

`y-30=(60-30)/(2-1)(x-1)`
`\begin{gathered} y-30\text{ = }(30)/(1)(x-1) \\ y-30=30x-30 \\ y=30x-30+30 \\ y=30x \end{gathered}`

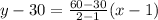
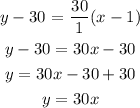
The equation that represents the cost of the topsoil is

y=30x

Step 3

Find how the cost of the topsoil compares to the cost of the mulch.

`\begin{gathered} \text{The equation for the cost of the mulch y, in dollars is} \\ y=25x \\ \text{for x cubic yards of mulch} \\ \text{The equation for the cost of topsoil, y in dollars is} \\ y=30x \\ for\text{ x cubic yards of topsoil} \end{gathered}`