Question

The length of a rectangle is 6 cm more than the width. If the perimeter is 52 cm. What are the dimensions of the rectangle?

Answer 1

LA rectangle has two pairs of sides of the same length. If we call W to the width of the rectangle, we know that the length is 6cm more. If we call L the length of the rectangle:

`L=W+6`

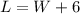
The perimeter of a rectangle is twice the length plus twice the width:

`Perimeter=2L+2W`

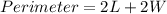
Since we know that the perimeter is 52 cm, we can write the system of equations:

`\begin{cases}L={W+6} \\ 2L+2W=52{}\end{cases}`

We can substitute the first equation into the second one:

`2(W+6)+2W=52`

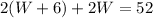
And solve:

`2W+12+2W=52`
`\begin{gathered} 4W=52-12 \\ . \\ W=(40)/(4)=10\text{ }cm \end{gathered}`

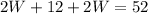
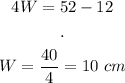
We know that W = 10cm, we can now find L:

`L=10+6=16\text{ }cm`

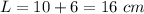
Thus, the dimensions of the rectangle are:

Length: 16 cm

Width: 10 cm